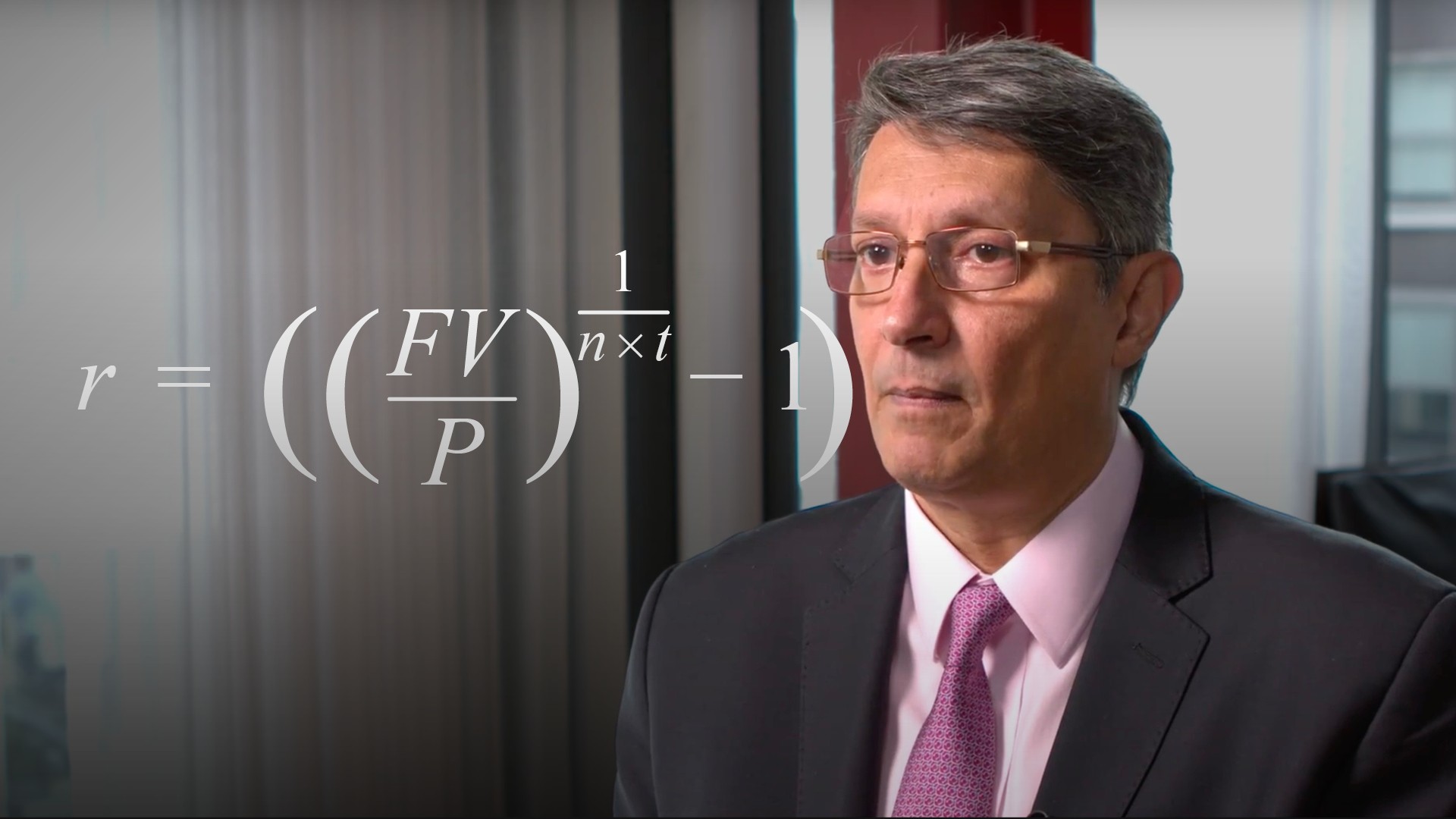
Calculating Continuously Compounded Rates of Returns

Abdulla Javeri
30 years: Financial markets trader
Continuously compounded rates of return are widely used in financial markets, especially in the world of derivatives. In this video, Abdulla outlines the concept and provides some examples framed as investment returns.
Continuously compounded rates of return are widely used in financial markets, especially in the world of derivatives. In this video, Abdulla outlines the concept and provides some examples framed as investment returns.
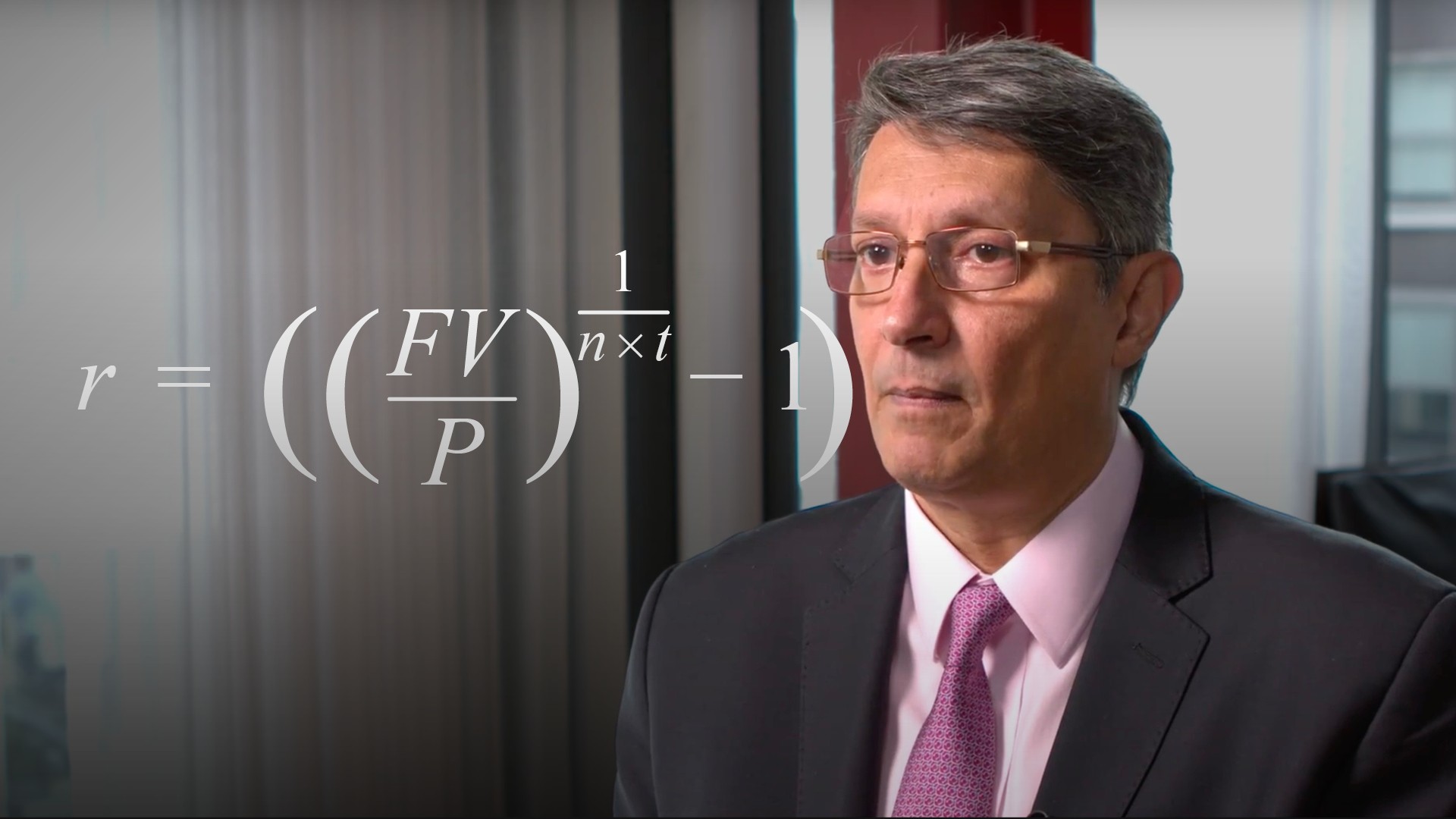
Calculating Continuously Compounded Rates of Returns
5 mins 3 secs
Key learning objectives:
Define continuous compounding
Calculate both the continuously compounded rate of return, and the future value of an investment
Overview:
Continuously compounded rates of return are widely used in financial markets, especially in the world of derivatives. They are typically useful when dealing with returns on assets whose price cannot fall below zero.
What are investment returns?
- Usually measured as a percentage rate
- Can be calculated for the holding period, or on an annualised basis
- Can be calculated on a discrete basis, or on a continuously compounded basis
What is a discrete return?
If we start with an initial investment of 100, which a year later is worth 110, we’ve earned a discrete return of 10% a year. A profit of 10, on our original starting point of 100.What is continuous compounding?
Continuously compounding is essentially investing for an immeasurably small period, and re-investing both principal and return for an infinite number of immeasurably small periods until the end of the year, and we need to find the rate that gets us from 100 to 110.What is the generic compounding formula, and why won’t it work?
P x (1+r/n)n x t = FV
Can be re-arranged to solve for r
r = ((FV/P)(1/(n x t))-1) x n
With continuous compounding, n approaches infinity - so this formula won’t work.
What formula can we use that fixes the n = infinity issue?
P x Er x t = FV
Can be re-arranged to solve for r
r = In(FV/P)/t
Using the information below, how do we calculate the compounded rate of return and the future value?
- P = Principal (100)
- r = Annual rate of return
- n = Number of compounding periods in a year
- r/n = Rate for the period - the periodic rate
- t = Time in years (1)
- n x t = Number of compounding periods
- FV = Future value of principal (110)
- Continuously compounded rate of return: ln(110/100)/1 = 0.953102. Hence, if we invest at about 9.53% a year, on a continuous basis, we will move from 100 at the beginning of the year to 100 at the end of the year.
- Future Value (FV): 100(e0.953102) = 110

Abdulla Javeri
There are no available Videos from "Abdulla Javeri"

