
FX Options Case Study

Lindsey Matthews
30 years: Risk management & derivatives trading
In this video, Lindsey explains how to price a EUR put - USD call and GBP call - CHF put.
In this video, Lindsey explains how to price a EUR put - USD call and GBP call - CHF put.

FX Options Case Study
10 mins 59 secs
Key learning objectives:
Understand how to price a EUR put - USD call
Understand how to price a GBP call - CHF put
Overview:
FX forwards and options are trades where a currency pair is exchanged in the future, at a price agreed on today. The calculation of the forward price is similar to calculating the forward price on an equity option, however, the costs will be in one of the currencies and the benefits will be in the other. Run through the case studies in this video for a deeper understanding.
How would you price a EUR put - USD call?
If we were to buy 10 million of the 3-month $1.35 strike EUR put - USD call, what would we have bought?
It is an option on the euro dollar, so the euro is the currency that we are buying and selling, i.e. €10m. The option is a put, so it is an option to sell €10m at a strike price of $1.35.
At expiration, if EUR-USD ends up below $1.35, we would exercise the option and receive $13.5 million in exchange for the €10 million.
Now we understand what the option is, we can value it.
Assume the 3-month forward on EUR-USD is 1.3485, and EUR-USD volatility is 7%. We can build the distribution using Lindsey’s simple option pricing model and calculate the value at expiry as shown in the diagram:
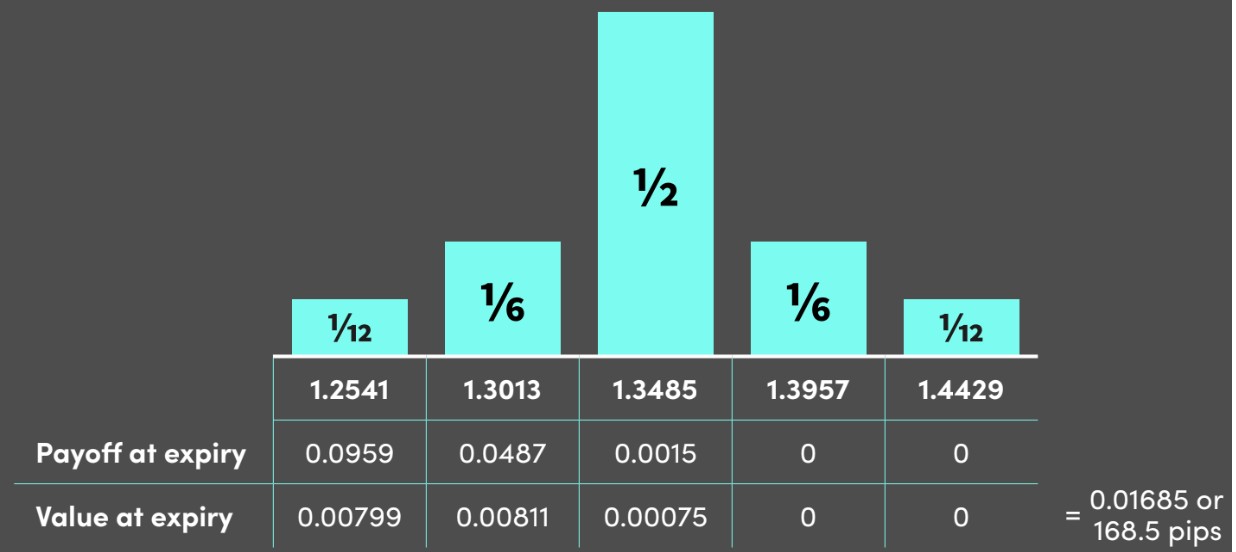
Given this is an option on EUR - USD, the prices are in dollar terms.
How would you price a GBP call - CHF put?
This example is from interest rates were much higher.
In July 2001, GBP/CHF was trading at 2.4603, the GBP 2-year rate was 5.64% and the 2-year CHF rate was 3.07%. The 2-year forward was 1190 pips lower at 2.3413 and volatility is at 8.4%.
Let’s say we want to value the at-the-money options. We can calculate this using the simple model for ATMF options using the approximation Lindsey outlined in an earlier video:
0.4 x 2.3413 x 8.4% x sqt(2) = 0.11411
Discounting this back using the Swiss rate of 3.07% gives:
0.1111 / 1.0307^2 = 0.1047 or 1047 pips

Lindsey Matthews
There are no available Videos from "Lindsey Matthews"

