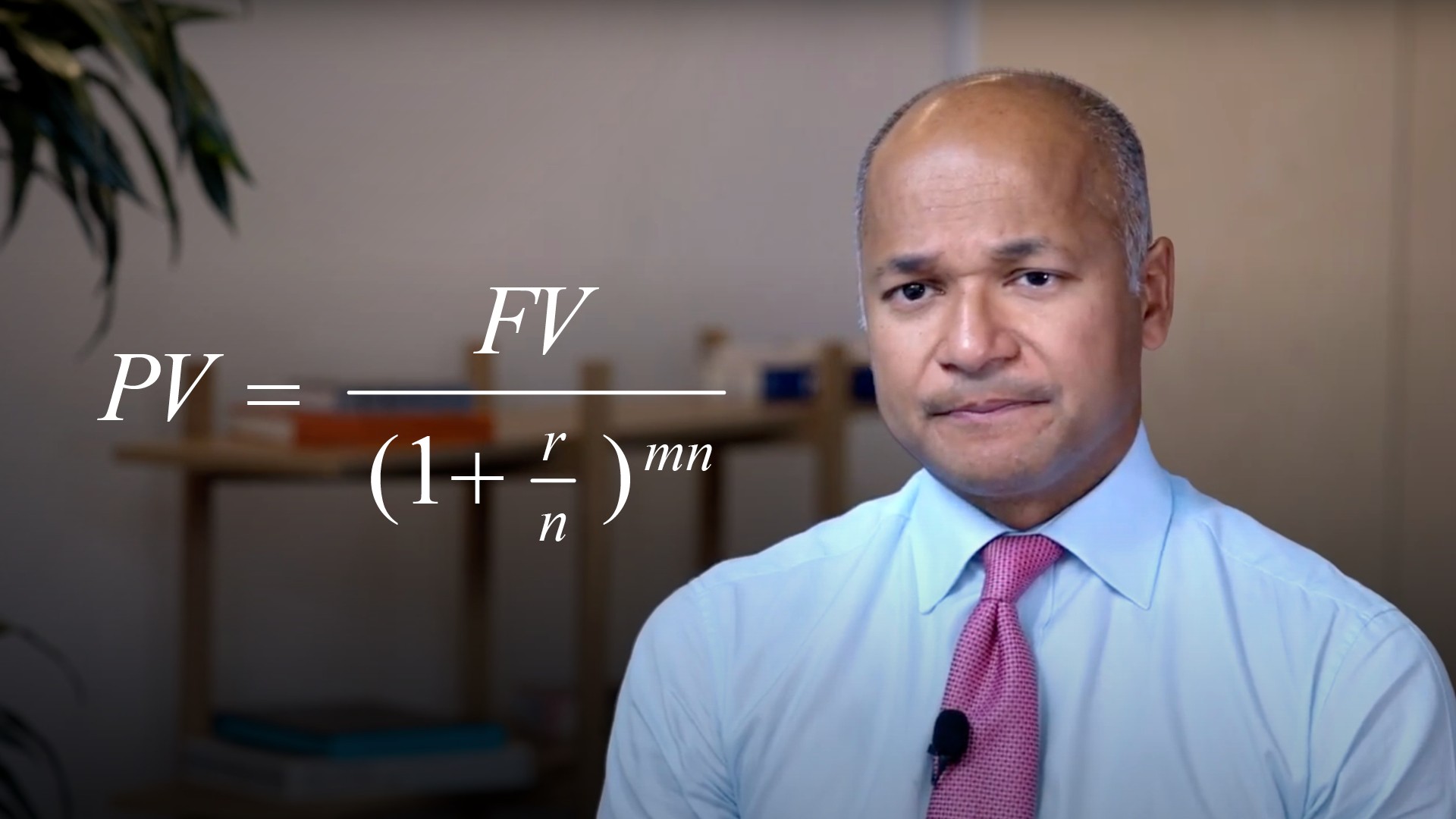
Effective Interest Rates and Discount Factors
Moorad Choudhry
25 years: Treasury & ALM
In this second part of Moorad's introduction to the time value of money, he explains effective interest rates, present value and discount factors.
In this second part of Moorad's introduction to the time value of money, he explains effective interest rates, present value and discount factors.
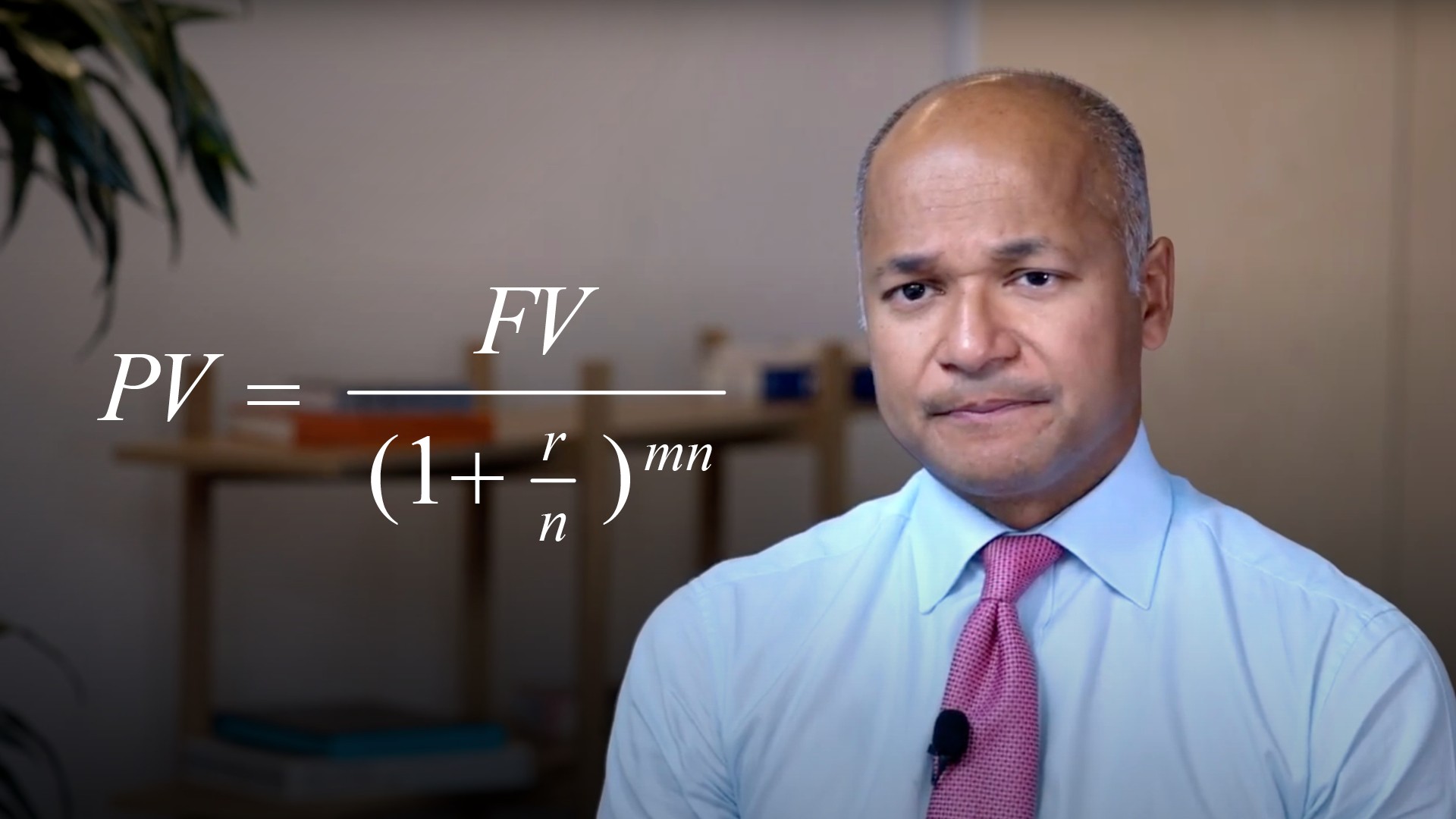
Effective Interest Rates and Discount Factors
9 mins 56 secs
Overview
This further explanation of the time value of money includes calculations of effective rates, present value and the use of discount factors.
Key learning objectives:
Understand the need and use of effective interest rates
Use discount factors to calculate the present value
Summary
Expert
Moorad Choudhry
Former senior banker with almost 30 years experience. Moorad has held senior roles in commerical, investment and retail banking. He has also spent the last five years as a visiting professor.
Related videos
