Introduction to the Monte Carlo Simulation

Abdulla Javeri

30 years: Financial markets trader

Abdulla explains the significance of the Monte Carlo Simulation: what it tries to achieve and how it works. In so doing, Abdulla provides an example using an excel spreadsheet.

Financial Maths

Abdulla explains the significance of the Monte Carlo Simulation: what it tries to achieve and how it works. In so doing, Abdulla provides an example using an excel spreadsheet.

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Introduction to the Monte Carlo Simulation

4 mins 52 secs

Key learning objectives:

Describe the Monte Carlo Simulation
Outline some of its uses in financial markets
Understand how the simulation works in practice

Overview:

The Monte Carlo Simulation is a technique used to stimulate potential changes to a value, a price, or any number, usually over a number of time periods. It has a wide variety of applications, some of which include: stock prices and inflation rates.

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Summary

What is the Monte Carlo Simulation?

A method used to stimulate a unique path for potential changes to a number
Based on a random pick from an assumed probability distributed with a mean and standard deviation
When repeated numerous times it defines the probability distribution of the final outcomes

Under which conditions can the simulation be used?

Essentially it can be used in any area where numbers are subject to change, but where the change is not perfectly predictable, or is subject to some randomness in its movement.

What are some of its uses in financial markets?

Valuation of certain types of options
Potential changes to the price of assets over time
In the measurement and management of risk

What does the Monte Carlo method require?

An average for the expected change
A standard deviation/volatility

How does the simulation work in practice?

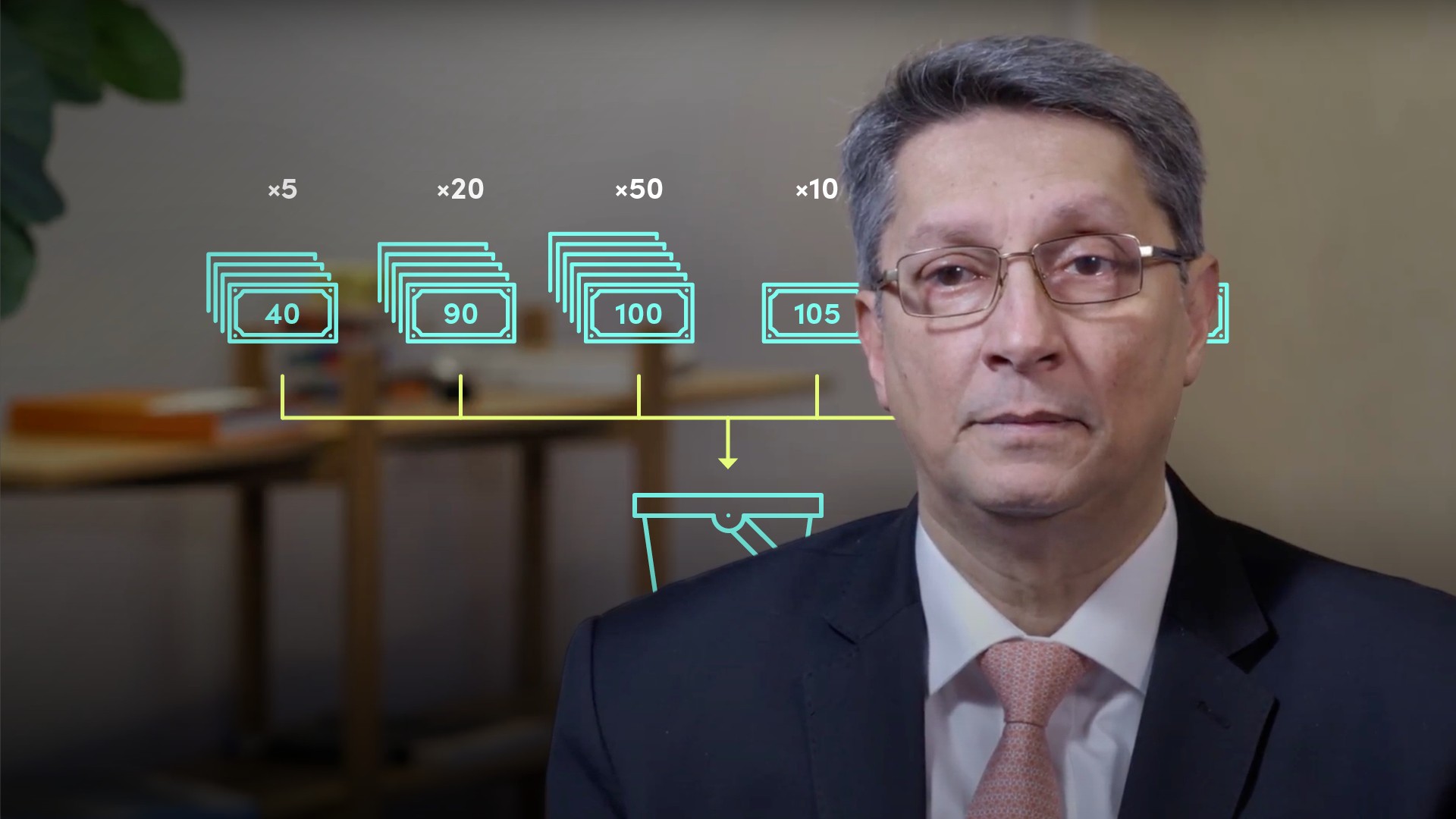
Today’s value = 100. We want to know what the number could potentially be tomorrow: let's assume that tomorrow we expect the number to remain unchanged, but subject to some variability. Assume that it could be any of the numbers in the figure below - The probabilities associated with those numbers are also shown:

As shown in the graphic above, take 100 pieces of paper, and write one outcome on each piece reflecting the probabilities of each outcome. Put them all in a bucket, and pick one at random. This will give you the next potential measurement. Every time you take a random pick, you’ll get a different outcome, hence reflecting the nature of the distribution

As to where the averages and probabilities come from, we can get the distribution of prices from historic data, or make rational assumptions about them

We can repeat this as many times as needed, and hence generate a simulated path for changes to the original number

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Abdulla Javeri

Abdulla’s career in the financial markets started in 1990 when he entered the trading floor of the London International Financial Futures Exchange, LIFFE, and qualified as a pit trader in equity and equity index options. In 1996, Abdulla became a trainer for regulatory qualifications and then for non-exam courses, primarily covering all major financial products.

There are no available Videos from "Abdulla Javeri"