Options Valuation Exercises

Lindsey Matthews

30 years: Risk management & derivatives trading

In this video, Lindsey explains the application of the simple valuation model to value 4 options

Financial Markets

In this video, Lindsey explains the application of the simple valuation model to value 4 options

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Options Valuation Exercises

3 mins 53 secs

Key learning objectives:

Apply the simple valuation model to value 4 options

Overview:

To establish the model distribution you require the forward price and the volatility. The forward price is $1,000 and the 3-month volatility is 5%. What is the value of the $1,000 call? What is the value of the $1,000 put? What is the value of the $1,025 call? What is the value of the $1,025 put?

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Summary

What is the value of the $1,000 call?

First, calculate the payoff at expiry. Only the $1,050 and $1,100 bars are in the money, with $50 and $100 payoffs respectively.

Second, calculate the value at expiry by multiplying by its probability, which results in a value of $8.33 for both bars in the money, resulting in an overall value of $16.66.

What is the value of the $1,000 put?

First, calculate the payoff at expiry. Only the $900 and $950 bars are in the money, with $100 and $50 payoffs respectively.

Second, calculate the value at expiry by multiplying by its probability, which results in a value of $8.33 for both bars in the money, resulting in an overall value of $16.33.

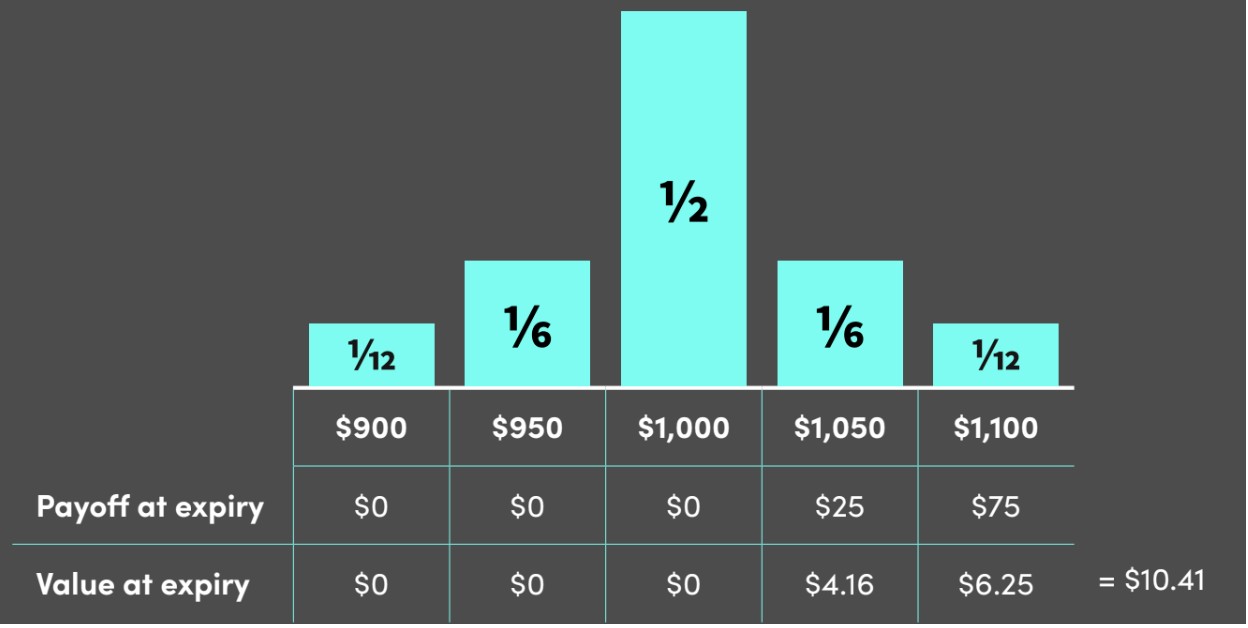
What is the value of the $1,025 call?

First, calculate the payoff at expiry. Both the $1,050 and $1,100 bars are in the money and have a $25 and $75 payoff respectively.

Second, calculate the value at expiry by multiplying by its probability, which results in a value of $4.16 for the $1,050 bar and $6.25 for the $1,100 bar, resulting in an overall value of $10.41.

What is the value of the $1,025 put?

First, calculate the payoff expiry. Both the $900, $950, and the $1,000 bars are in the money, with $125, $75 and $25 payoffs respectively.

Second, calculate the value at expiry by multiplying by its probability, which results in a value of $10.41, $12.50 and $12.50 at each point respectively, resulting in an overall value of $35.41.

Speak to an expert

Speak to an expert today to access this and all of the content on our platform.

Lindsey Matthews

Lindsey runs Perfordiant, an investment risk and performance consulting firm. He has worked in financial markets since 1992. Lindsey became an MD in fixed income and equities, ran a Risk function, and was on the management team of an Asset Management fintech business. Lindsey is now a Visiting Fellow at the Henley Business School, and resides on the board of CFA UK.

There are no available Videos from "Lindsey Matthews"