What is Linear Regression?

Abdulla Javeri
30 years: Financial markets trader
This video is a continuation in the series where Abdulla examines whether movements in one asset are somehow related to movements in another asset. The subject of this video is linear regression, otherwise known as simple linear regression or least squares regression.
This video is a continuation in the series where Abdulla examines whether movements in one asset are somehow related to movements in another asset. The subject of this video is linear regression, otherwise known as simple linear regression or least squares regression.

What is Linear Regression?
4 mins 55 secs
Key learning objectives:
What is linear regression?
How do you construct a regression line?
How do you define the slope of the line?
Overview:
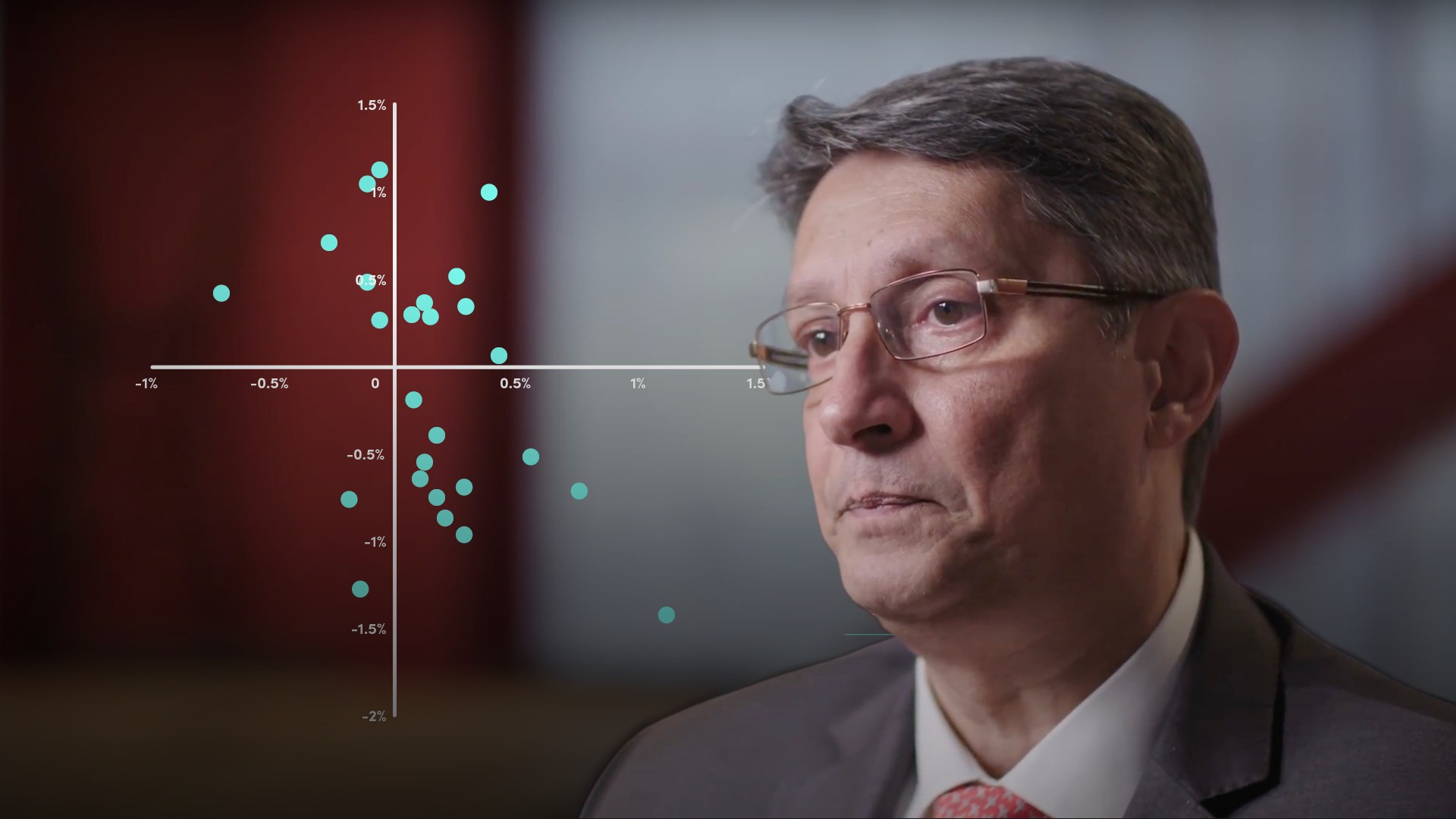
Linear regression, also known as simple linear regression or least squares regression, attempts to quantify the expected return for one asset given the return for another asset. The regression line defines the relationship between the expected return for a particular asset (defined as the dependent variable) and another asset (defined as the independent variable). The line passes through the average of both, with a slope that minimises residual errors.
What is linear regression?
Linear regression, also known as simple linear regression or least squares regression, attempts to quantify the expected return for one asset given the return for another asset. The regression line defines the relationship between the expected returns for a particular asset defined as the dependent variable, and another asset defined as the independent variable. It’s the line that passes through the average of both, with a slope that minimises the residual errors.
To define a regression line requires data, e.g. gold vs the euro, gold vs the Dow Jones equity index where relationships look linear. Non-linear relationships can still be represented in linear form, but regression analysis will likely have very large errors.
How do you construct a regression line?
To construct a regression line, calculate the average daily return of a given company’s shares. (The average daily return offers the best expectation of future daily returns). Error terms or residuals (the differences between the actual returns and the expected return) can be quantified by summing the squares of each residual a.k.a. the sum of squared errors (SSE).
Bringing in another asset that might have a relationship to the first asset in terms of returns and calculating its movements could explain some of the errors in the first dataset, say comparing Apple (the dependent variable) to returns on a market index (the independent variable). The regression line must satisfy two conditions:
- It must go through the average return for Apple and the average return for the market
- The slope of the line must minimise the remaining residuals or errors
How do you derive the slope of the regression line?
The slope of the regression line is derived from measuring the SSE and rotating the line until the smallest SSE is reached. This should be smaller than the original SSE for our company’s shares, providing some explanation for those errors. This shows in a linear form the relationship between the expected returns for that company versus the market. The y axis is the expected return on the company’s shares, which is the return for the market multiplied by b (the gradient or slope) + plus c the intercept.
Abdulla Javeri
There are no available Videos from "Abdulla Javeri"

