Is the Regression Line Appropriate (or Good Fit)?

Abdulla Javeri
30 years: Financial markets trader
From a financial markets perspective, linear regression is described as a way of looking at the relationship between returns on two assets. In this video, Abdulla demonstrates how to calculate the regression line, and evaluates its value as an estimator.
From a financial markets perspective, linear regression is described as a way of looking at the relationship between returns on two assets. In this video, Abdulla demonstrates how to calculate the regression line, and evaluates its value as an estimator.

Is the Regression Line Appropriate (or Good Fit)?
4 mins 22 secs
Key learning objectives:
Identify what determines if beta is a good fit
Learn how to calculate errors of a regression
Overview:
Beta might not be a reliable measure given the inaccuracy between a regression analysis and the actual data. The following walks us through how to calculate the errors.
What does the regression line tell us?
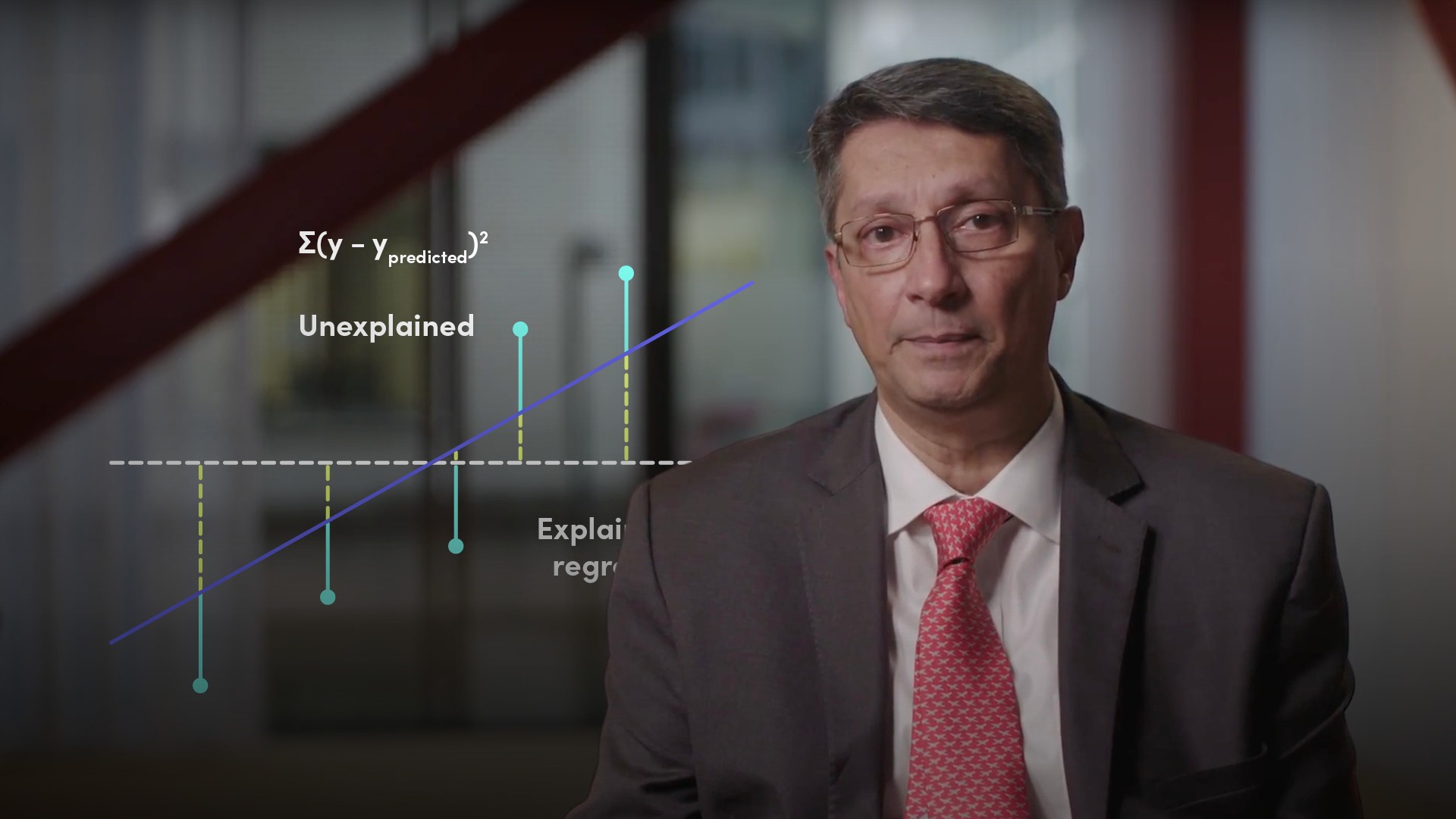
From a financial markets perspective, the story with linear regression so far is that it’s a way of looking at the relationship between returns on two assets. The regression line is the line of best fit, in other words it’s the line that minimises the sum of squared errors, or the residuals. In financial markets we refer to the slope of the line as beta.
How do we calculate the errors of a regression?
We calculate the total error by taking the difference from the actual data point to the average and squaring. Repeat for each data point and add them all up. That gives the sum of squared errors, which in this case, we're calling the total sum of squares SST as it’s our starting point. At the moment, the errors are unexplained.
Next, bring in a second variable x and introduce the regression line to see whether we can explain some of those errors. We now re-calculate the sum of squared errors which we’ll call SSE. This time, instead of going from actual to the y average, we are going from actual to y predicted by the regression line. The re-calculated SSE is the amount of the error that’s still unexplained. The rest of it compared to the total sum of squares SST, can be assigned to, or explained by, the regression. The explained portion we call the sum of squares due to regression SSR. So, SST equals SSE plus SSR.
What determines if beta is a good fit?
We can also get the coefficient of determination by squaring the correlation. That’s r squared. A high r squared number equates to a good fit. What defines a high r squared? Well, that’s a matter of judgement.
What conclusions can we draw?
So, in conclusion, it’s reasonably straightforward to calculate the regression line, but, before using it with any confidence as an estimator, we’ve got to check whether it’s appropriate or whether it’s a good model to start with.

Abdulla Javeri
There are no available Videos from "Abdulla Javeri"

