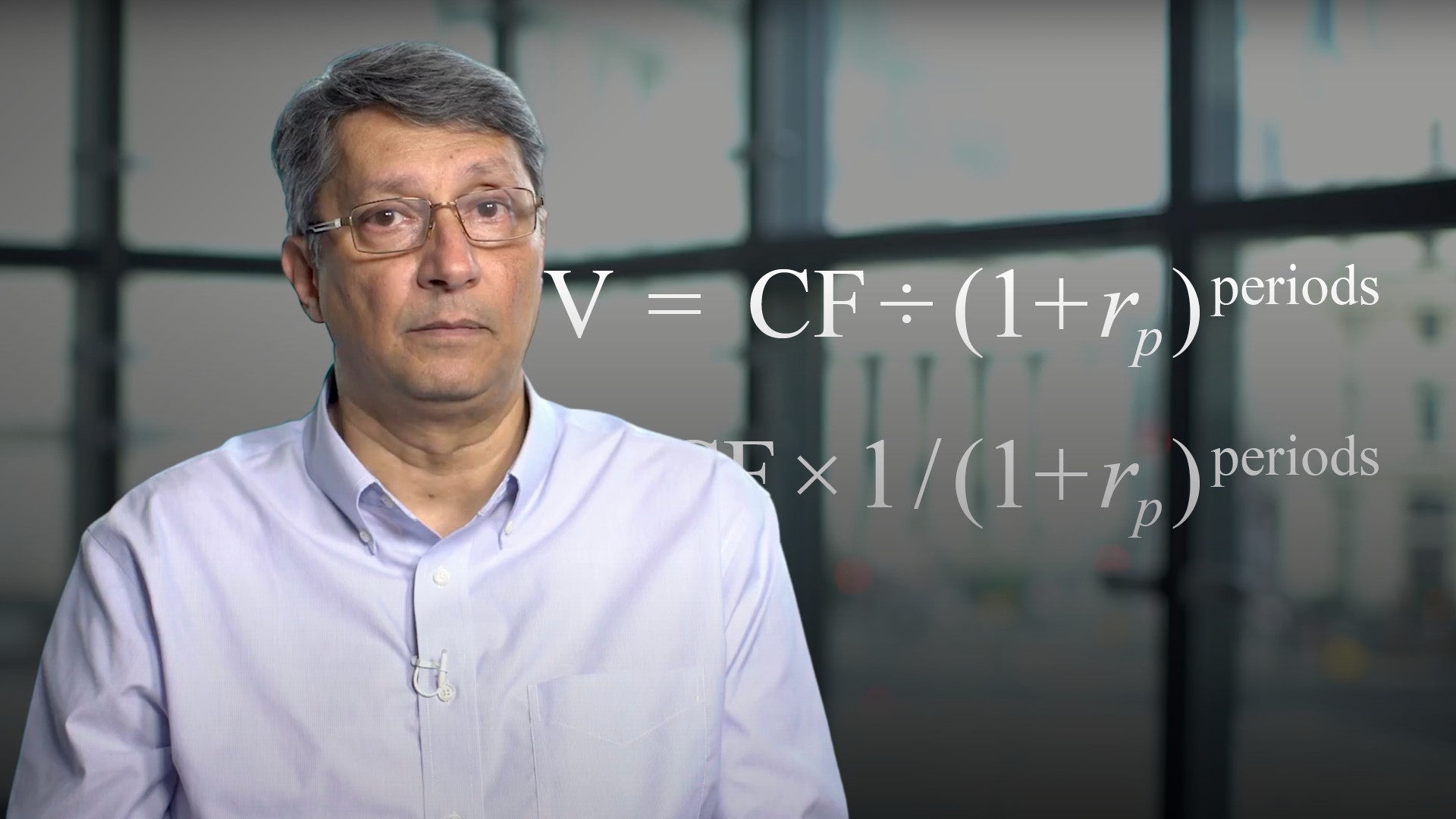
Discount Factors (Bonds)

Abdulla Javeri
30 years: Financial markets trader
Discount factors are crucial in valuing cash flows, financial assets including derivatives on a consistent and accurate basis. In this video, Abdulla explains how they are applied using bond markets as an example.
Discount factors are crucial in valuing cash flows, financial assets including derivatives on a consistent and accurate basis. In this video, Abdulla explains how they are applied using bond markets as an example.
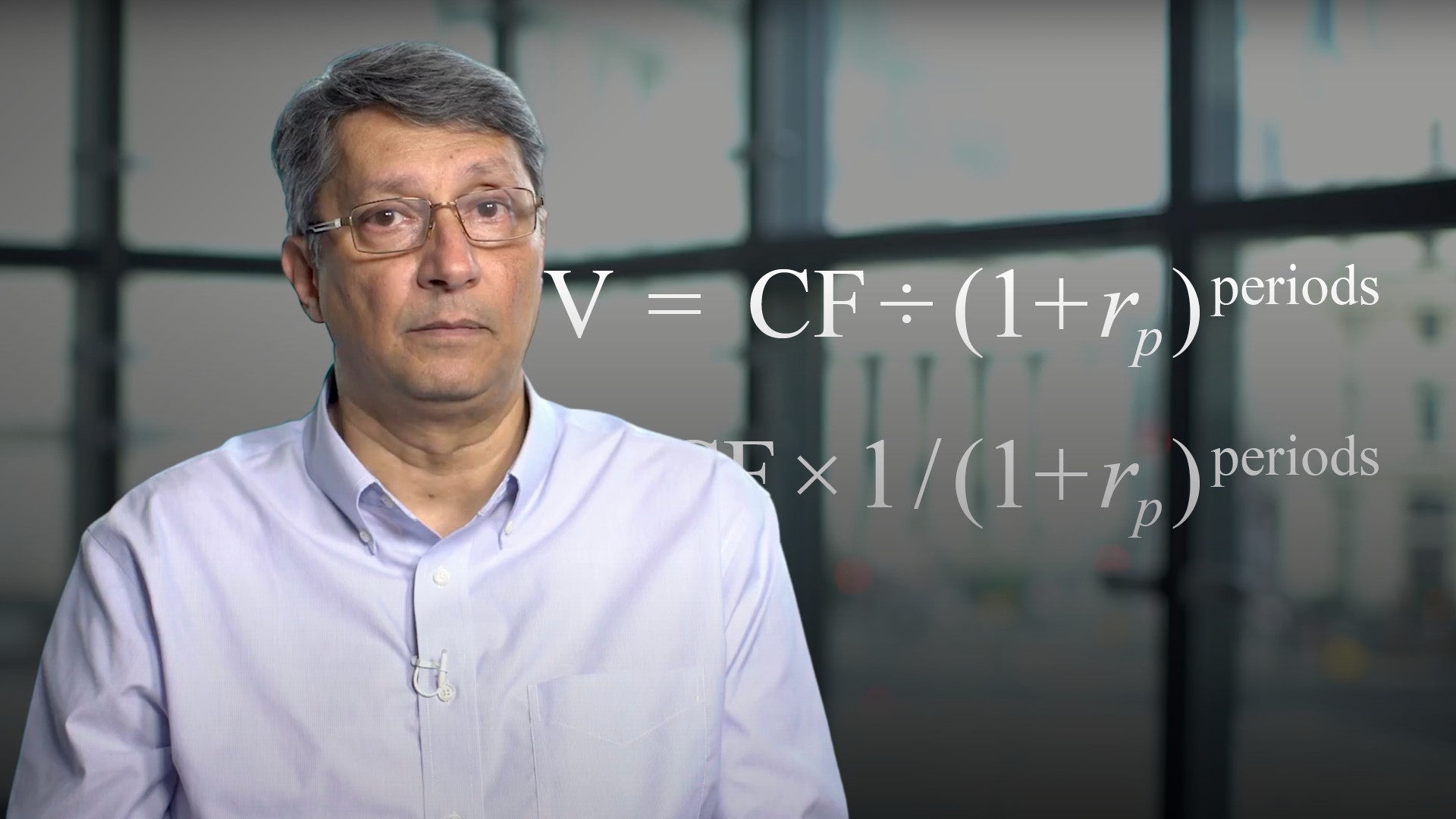
Discount Factors (Bonds)
4 mins 19 secs
Key learning objectives:
How should discount factors be applied using bond markets as an example?
Overview:
Bond markets often require multi-period discount factors, which can be calculated by adjusting the basic discounted cash flow equation.
How should discount factors be applied using bond markets as an example?
The basic TVM formula to solve for the present value of cash flows receivable or payable in the future is as follows:
PV = CF/(1+rp)periods
Rp is the rate for the period i.e. a rate or yield-to-maturity on a bond, divided by n, the frequency of interest or coupon payments in a year – rate(yield)/n. For a bond paying annual coupons, n is 1; for semi-annual n is 2; for quarterly n is 4.
The exponent is n multiplied by the time in years to the cash flow i.e. for a cash flow occurring in two years on a bond paying annual coupons, n is 1 and t is 2, so the power is 2. If it’s a semi-annual paying bond and the cash flow occurs in three years, n is 2 and t is 3 so the number of periods in the exponent, in this case, is 6.
The formula can be rearranged such that the PV is the future cash flow multiplied by 1 over 1 plus the periodic rate to the power of periods. We can calculate the latter expression separately and that’s the discount factor. What we’re left with is that the present value is the future cash flow multiplied by its discount factor.
The formula can be rewritten as:
PV = CF x 1/(1+rp)periods

Abdulla Javeri
There are no available Videos from "Abdulla Javeri"

